Bihar Board Class-9 Number System Solution Exercise-1.4, 1.5

                      प्रश्नावली-1.4

1. उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए|

उत्तर:—

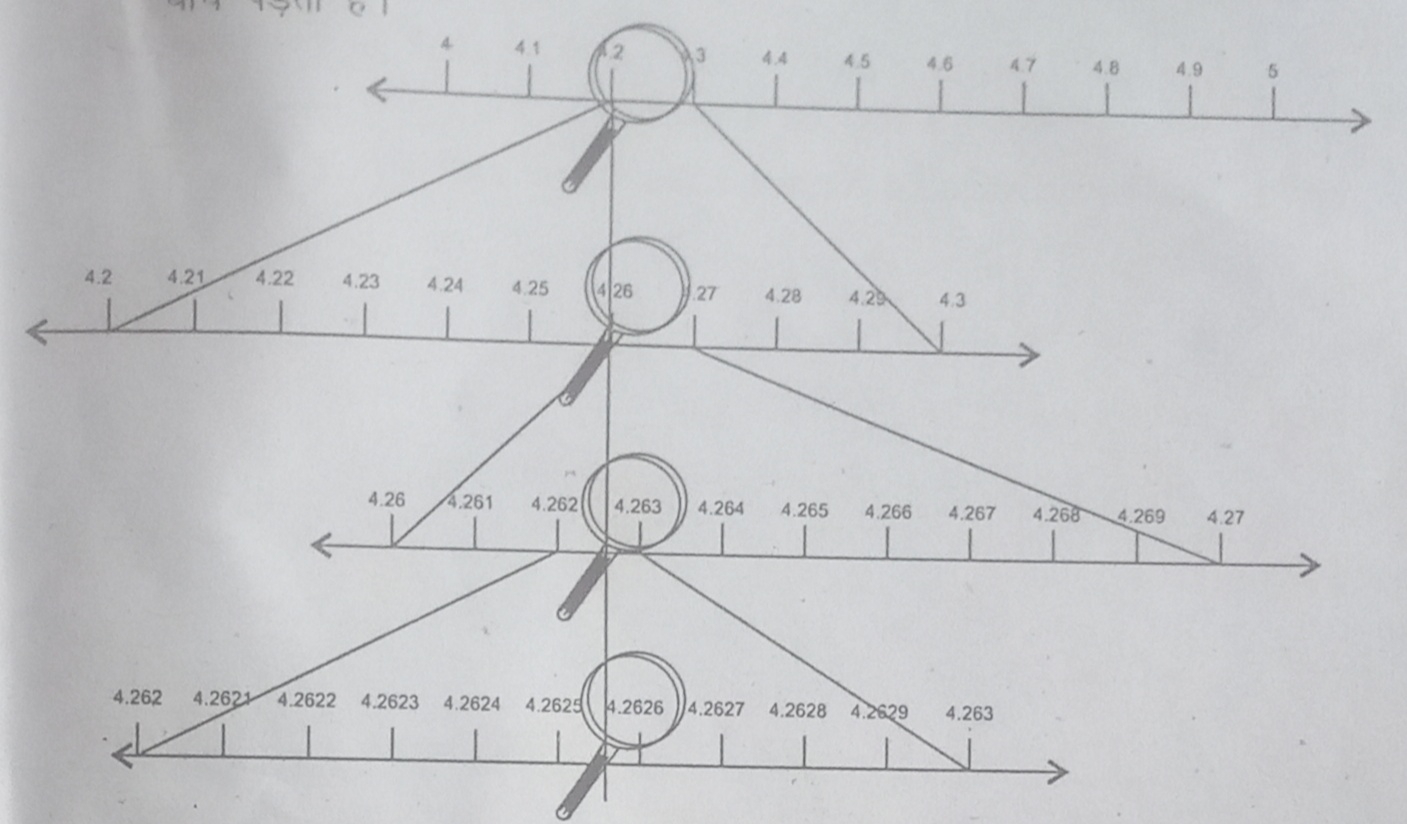
2. दशमलव स्थानों तक संख्या रेखा पर 4.26 को देखिए|

उत्तर:—

                         प्रश्नावली-1.5

1. बताइए कि नीचे दी गई संख्याओं में कौन परिमेय है और कौन अपरिमेय है? 

(i) 2 -√5 (ii) (3+√23)-√23  (iii)   2√7  

                                                     7√7

(iv)   1       (v) 2π

        √2

उत्तर:—

(i) अपरिमेय

(ii)  परिमेय

(iii) परिमेय

(iv) अपरिमेय

(v) अपरिमेय

2. निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए|

(i) (3+√3) (2+√2)   (ii)(3+√3)(3-√3)

(iii)(√5+√2)2   (iv)(√5-√2)(√5+√2

उत्तर:—

(i) (3+√3)(2+√2)=3×2+3×√2+√3×2

+√3×√2=6+2√3+3√2+√6

(ii)(3+√3)(3-√3)=3×3-√3×√3=9-3=6

(iii)(√5+√2)2=(√5)2+2×√5×√2+(√2)2

=5+2√10+2=7+2√10

(iv) (√5-√2)(√5+√2)=√5×√5-√2×√2

=5-2=3

3. आपको याद होगा कि π को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिएd) के अनुपात से परिभाषित किया जाता है, अर्थात π=c/d है| यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि अपरिमेय है| इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे? 

उत्तर:—

इसमें कोई अंतर्विरोध नहीं है| हम स्मरण करें कि जब हम किसी स्केल या कोई अन्य उपकरण से किसी लंबाई को मापते है तो हमें सिर्फ लगभग (अति समीप) परिमेय मान का पता चलता है| इसिलिए, हम यह नहीं महसूस कर पाते या जान पाते हैं कि या तो c या d अपरिमेय है| अगर c या d अपरिमेय है, तो यह निश्चित है कि एक परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल सदैव अपरिमेय संख्या ही है| दूसरी तरफ यदि c और d दोनों अपरिमेय होंगे तो उनका गुणनफल भी अपरिमेय ही होगा| लेकिन इस स्थिति में, गुणनफल का सदैव अपरिमेय होना जरूरी नहीं है|

4. संख्या रेखा पर √9.3 को निरूपित कीजिए|

उत्तर:—

एक रेखाखंड AB खींचते है जो AB=9.3 इकाई है और इसे C तक बढ़ा देते हैं ताकि BC=1 इकाई| तब AC रेखाखंड पर O, AC का मध्य बिंदु निश्चित कर देते हैं| O केन्द्र मानकर और OA त्रिज्या से एक अर्द्ध वृत्त खींचते है| अब DB|AC खींचते है जो कि अर्द्ध वृत्त को D पर काटता है| तब BD =√9.3 , इकाई| B को केन्द्र मानते हुए तथा BD त्रिज्या लेकर एक चाप खींचते है जो के बढ़े भाग को E बिंदु पर प्रतिच्छेद करता है| इस प्रकार √9.3 को बिंदु निरूपित करता है|

5. निम्नलिखित के हरों का परिमेयकरण कीजिए|

उत्तर:–

(i)  1   =  1   ×  √7  =  √7   

    √7      √7      √7      7

(ii)      1        =     1     ×  √7+√6 

       √7-√6       √7-√6     √7+√6

=   √7+√6       =√7+√6

        7-6

(iii)       1       =     1      ×   √5+√2   

         √5-√2       √5-√2     √5+√2

=   √5+√2        =   √5+√2    

       5-2                    3

(iv)     1     =     1      ×    √7+2    

       √7-2       √7-2          √7+2

=    √7+2       

      7-4=3